Problem Based On The Coefficient Of The Binomial Theorem Part 2

Problem Based On The Coefficient Of The Binomial Theorem Part 2 The binomial coefficient (n k) represents the number of combinations of n objects taken k at a time, and is read “ n choose k. we would now like to investigate the relationship between permutation and combination problems in order to derive a formula for (n k) let us reconsider the counting with no order, example 2.4.2. We can see these coefficients in an array known as pascal's triangle, shown in figure 13.6.2. figure 13.6.2. to generate pascal’s triangle, we start by writing a 1. in the row below, row 2, we write two 1 ′ s. in the 3 rd row, flank the ends of the rows with 1 ′ s, and add 1 1 to find the middle number, 2.

Solution Binomial Theorem Part 2 Studypool Analysis . notice that we obtained the same result for parts (b) and (c). if you look closely at the solution for these two parts, you will see that you end up with the same two factorials in the denominator, but the order is reversed, just as with combinations. Ger, the numbersn n!=k k!(n − k)!are the binomial coefficients, and n! denotes the factorial of n.this formula, and the triangular arrangement of. the binomial coefficients, are often attributed to blaise pascal who describe. , here are the cases n = 2, n = 3 and n =. n integer), and. the coe. Properties of binomial expansion. the first term and last term of the expansion are an a n and bn b n, respectively. there are n 1 n 1 terms in the expansion. the sum of the exponents of a a and b b in any term is n n. the exponent of a a decreases by 1 1, from n n to 0 0. the exponent of b b increases by 1 1, from 0 0 to n n. The binomial theorem is a formula for expanding binomial expressions of the form (x y) n, where ‘x’ and ‘y’ are real numbers and n is a positive integer. the simplest binomial expression x y with two unlike terms, ‘x’ and ‘y’, has its exponent 0, which gives a value of 1. (x y) 0 = 1. if the exponent is increased by 1, (x.

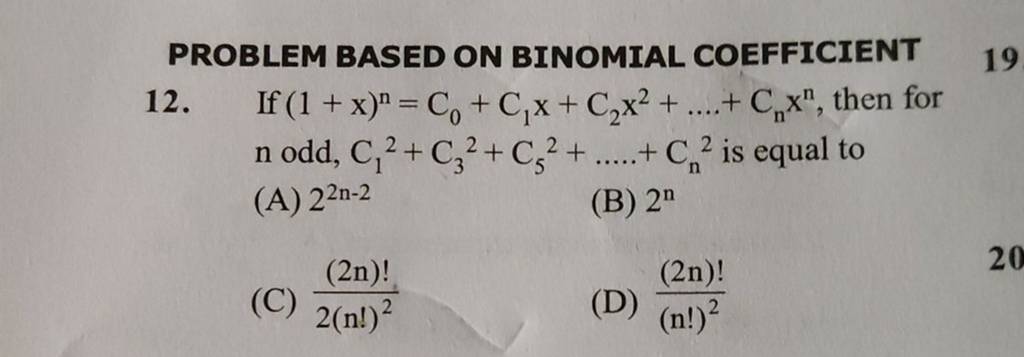
Problem Based On Binomial Coefficient 12 If 1 X N C0 C1 X C2 X2 вђ Cn Properties of binomial expansion. the first term and last term of the expansion are an a n and bn b n, respectively. there are n 1 n 1 terms in the expansion. the sum of the exponents of a a and b b in any term is n n. the exponent of a a decreases by 1 1, from n n to 0 0. the exponent of b b increases by 1 1, from 0 0 to n n. The binomial theorem is a formula for expanding binomial expressions of the form (x y) n, where ‘x’ and ‘y’ are real numbers and n is a positive integer. the simplest binomial expression x y with two unlike terms, ‘x’ and ‘y’, has its exponent 0, which gives a value of 1. (x y) 0 = 1. if the exponent is increased by 1, (x. Generalized binomial theorem the binomial theorem is only truth when n=0,1,2 , so what is n is negative number or factions how can we solve. the binomial theorem: =σ =0 − the generalized binomial theorem: 1 𝑟=෍ =0 ∞ , ∈ℝ. The real beauty of the binomial theorem is that it gives a formula for any particular term of the expansion without having to compute the whole sum. let’s look for a pattern in the binomial theorem. notice, that in each case the exponent on the b is one less than the number of the term. the (r 1) s t (r 1) s t term is the term where the.